The Future of Artificial Intelligence is Self-Organizing and Self-Assembling
This is the first post in a series I plan to write on the work from our group and others that combines ideas from deep learning with ideas from self-organization and collective systems. In this first post, we’ll look at some of the developed approaches and the domains they have been applied to, ranging from growing soft robots and Minecraft machines to self-assembling modular robots, and creating more resilient and adaptive reinforcement learning agents. The merger of these ideas could ultimately allow our AI systems to escape their current limitations such as being brittle, rigid, and not being able to deal with novel situations. However, the combination of these methods also poses new challenges and requires novel ways of training to work as efficiently as possible.

One of the most fascinating aspects of nature is that groups with millions or even trillions of elements can self-assemble into complex forms based only on local interactions and display, what is called, a collective type of intelligence. For example, ants can join to create bridges or rafts to navigate difficult terrain, termites can build nests several meters high without an externally imposed plan, and thousands of bees work together as an integrated whole to make accurate decisions on when to search for food or a new nest. Surprisingly, achieving these incredible abilities is a result of following relatively simple behavioral rules and through a process of self-organization, which Camazine et al. (2001) define as:
“As a process in which pattern at the global level of a system emerges solely from numerous interactions among the lower level components of the system. Moreover the rules specifying interactions among the system’s components are executed using only local information, without reference to the global pattern. In short pattern is an emergent property of the system rather than being imposed on the system by an external ordering influence.“
Self-organizing systems are made out of many components that are highly interconnected. The absence of any centralized control allows them to quickly adjust to new stimuli and changing environmental conditions. Additionally, because these collective intelligence systems are made of many simpler individuals, they have in-built redundancy with a high degree of resilience and robustness. Individuals in this collective system can fail, without the overall system breaking down.
Multicellular organisms learned to exploit self-organizational principles to self-assemble, starting from a single egg cell and only through the process of local cell interaction during embryonic development. Similar to the robustness of swarms of organisms, the self-organization of cell populations is remarkably robust to perturbations. In some animals, this goes as far as being able to regenerate complete body parts, such as a salamander’s tail. This type of self-repair is a common feature of self-organizing systems and interestingly does not involve any additional processes:
“The same self-organization process that built the initial pattern can operate to repair the pattern.” — Camazine et al. (2001)
Self-assembly vs. Engineering
While evolution was able to exploit self-organizational processes to create artifacts of remarkable complexity, human-made designs are normally put together piece-by-piece, requiring external interventions to function again when being damaged (Edelmann et al. 2007). Indeed, the process of self-assembly is very different from the typical notion of construction in e.g. engineering (Davies 2014). To construct a building, architects first make a specific plan that shows the intended outcome. There is a hierarchy of commands to the people carrying out the work such as laying bricks, painting, etc. On the other hand, in biological construction, there is no clearly defined blueprint that shows the final structure. Instead, our genes contain the information to make the structure by controlling a sequence of events during morphogenesis.
The self-assembling process of biological nervous systems is also distinctively different from the way our current artificial neural networks are designed and trained. While biological networks are grown, artificial neural network architectures are typically constructed by humans and fine-tuned by an external and human-designed optimization algorithm (e.g. stochastic gradient descent). And while neural network-based approaches have shown amazing performance across many different domains, from e.g. playing StarCraft at grandmaster level (Vinyals et al. 2019) to protein folding (Jumper et al. 2021), current machine learning approaches often do not generalize well if confronted with situations not seen during training. Indeed, they currently do not display anywhere near the robustness of systems found in nature that exploit the principles of self-organization and self-assembly. In fact, artificial neural networks can often be fooled to make wrong predictions by only slight modifications of an image (Nguyen et al. 2015; Su et al. 2019). Other examples include deep reinforcement learning agents (Gleave et al. 2019) completely breaking down if confronted with an unknown player strategy in a soccer kick&defend environment (such as agents throwing themselves to the ground; a strategy that would be interesting to see in a real soccer game) or even just adding a few pixels to the screen of the Breakout video game (Qu et al. 2020).
While self-organization is not the only principle that allows biological organisms to display such high-level robustness – training in varying environments certainly seems like it is another important element (Stooke et al. 2021; Risi & Togelius 2020) – it likely is a key ingredient. Could our artificial neural networks and AI agents be made more robust and adaptable by incorporating ideas from collective intelligence systems such as self-organization? Stay tuned. We’ll return to this point later on.
One area of research that has already more readily embraced ideas from collective intelligence — such as self-assembly — is robotics. Here researchers have developed swarm systems, in which robots have to work together to solve tasks (Hamann 2018) such as assembling to traverse challenging terrain. A seminal example is the work by Rubenstein et al. (2014), in which a swarm of a thousand small robots called kilobots self-assemble into different target shapes solely based on the local communication between robots.
However, in Rubenstein et al.’s work, robots still relied on specific human-made algorithms to allow them to determine their position in the global coordinate system and to assemble into a desired shape. While we are still a long way from systems that can self-assemble into forms as complex as the ones seen in nature, or in the Disney movie Big Hero 6, with the emergence of powerful machine learning algorithms, the question is: can we instead of hand-designing algorithms for self-assembly, learn these algorithms instead, allowing more complex forms to be created?
Learning to Self-assemble
A model that naturally lends itself to studying self-organizing and developmental systems are Cellular Automata (CAs). Originally proposed in the 1940s (Neumann et al., 1966), Cellular Automata mimic developmental processes in multi-cell organisms including morphogenesis. A CA contains a grid of similarly structured cells, which are updated periodically in discrete time steps. At every time step, the status of each cell can be represented as a state, which is then transitioned into the next state per the update rule. The specific transition depends on the current state of the cell and the neighboring cells. Despite individual cells being simplistic, the entire CA is capable of complex behaviors. Below is an example of a 2D cellular automata called Conway’s Game of Life.
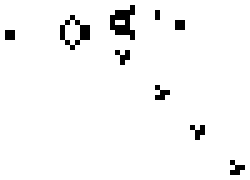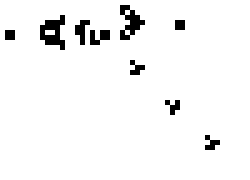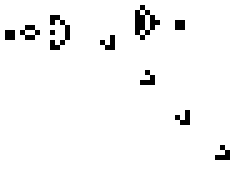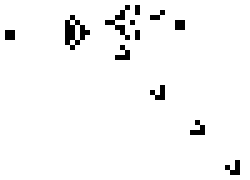
Cellular Automata can aid in the understanding of biological pattern formations (Wolfram, 1984), modeling of lattice-based physical systems in percolation and nucleation (Vichniac, 1984), and synthesis of artificial life (Langton, 1986).
Instead of hard-coded CA rules, in a Neural Cellular Automata (NCAs) (Wulff & Hertz, 1992), a neural network learns local rules based on communicating with its local neighbors, updating its internal state. In other words, the same neural network is applied to each grid cell, resembling the iterative application of a convolutional filter (Gilpin 2019). For example, in our work, we took inspiration from the evolution of developmental systems in nature and trained NCAs through an evolutionary algorithm to grow particular 2D patterns (Nichele et al. 2017). Here, the evolutionary algorithm trains both the NCA’s neural architecture and its weights. The input to the network are the states of the neighboring grid cells and the NCA’s fitness is determined by how closely the resulting pattern resembles the target pattern after a certain number of growth (i.e. developmental) steps.

While evolution is able to find NCAs that can successfully grow certain types of patterns, training to grow slightly more complex target structures (such as the Nordic flag in the figure above) has proven difficult. The reason for this is likely that the evolutionary optimization algorithm gets stuck in some local maxima of the complex fitness landscape imposed by such a developmental system. Addressing this problem, a recent approach by Mordvintsev et al. (2020) showed that, if a 2D target pattern is given, NCAs can be trained efficiently by supervised gradient descent to grow those patterns. Impressively, the system could also be trained to be very resilient to damage; almost the whole image can be removed and the system is able to regenerate. Similar to the biological inspiration (Camazine et al. 2001), the same process that grows the initial pattern is able to repair it.
One drawback of the previously mentioned NCAs is that they can only generate (and regenerate) the single artifact they are trained on, lacking the diverse generative properties of current probabilistic generative models. A very recent approach called a Variational Neural Cellular Automata mitigates this issue by using an NCA as the decoder in a VAE, enabling it to learn a purely self-organizing generative process of data.
From self-assembling static structures to functional machines
More recently we extended the approach of Mordvintsev et al. to 3D, utilizing 3D convolutions in the neural network architecture (Sudhakaran et al. 2021). Specifically, we developed a 3D NCA for generating 3D Minecraft structures and functional Minecraft machines. The NCA was trained to grow structures with up to 3,584 blocks and 50 unique block types through a series of reconstruction tasks. Minecraft proved to be a good test domain for our approach (and work on open-ended learning in general) because it allows the creation of both static (e.g. an oak tree) and dynamic (e.g. a moving caterpillar) structures. To generate dynamic structures, important block types are “piston” and “sticky piston” that push/pull other blocks if they are adjacent to a “redstone” block. “Slime” blocks glue to the adjacent blocks and pull them if the “slime” block gets pushed/pulled by a “piston” block. Our experiments show that, in most cases, NCAs scale to 3D effectively, able to grow complex entities from a single cell.
The NCAs also hold the same regenerative properties as their 2D counterparts. For example, we can cut a grown caterpillar in half and the other half will grow back into a fully functional caterpillar!
In the previous examples, the NCAs were tasked to grow a specific target structure. Can we train NCAs to grow structures with a specific function instead of pre-specifying a particular design? In some of our recent work (Horibe et al. 2021), we evolved NCAs capable of growing simulated soft robots able to locomote. Here the cells have to learn to communicate in order to decide which of four different materials they should become during the growth process. For example, red voxels can be thought of as muscles that actively contract and expand while other materials such as dark blue voxels are rigid and stiff. In addition to being able to find NCAs that grow morphologies capable to locomote, these robots are also capable of recovering from damage by partially regenerating their original morphology through local cell-to-cell interactions.
Self-assembling approaches have not to be restricted to 2D or 3D grid-like structures. Graph neural networks (Wu et al. 2020) generalize the idea of cellular automata to arbitrary graph structures (Grattarola et al. 2021). Recently Pathak et al. (2019) explored how to use reinforcement learning to train agents to self-assemble their morphologies with a dynamic graph network. Here modular robots are composed of small and primitive agents (consisting of a limb and a motor and resembling the modular robots from Big Hero 6), which can choose to link up with other agents. The resulting morphology of the assembled robot is then treated as a graph neural network, in which parameters are shared across limbs. Self-assembling agents are shown to generalize better to unseen environments and also to morphologies not seen during training, being composed of additional modules.
Self-organized Control
Exploiting ideas from self-organization has allowed approaches such as NCAs to create images, robot morphologies, and even functional Minecraft machines that are robust to damage and perturbations. Following the principles of biological self-organizing nervous systems that are incredibly flexible and adaptive, can we incorporate these ideas into our deep neural networks to endow them with similar benefits? Combining self-organizational principles with machine learning models goes back to the 1980s; a prominent example are self-organizing maps (SOMs), an unsupervised learning approach that builds on abstractions of biological networks and biological morphogenesis. More recently, our group and others have started to explore these questions in the realm of reinforcement learning.
For example, instead of optimizing the weight parameters of neural networks directly, only meta-learning synapse-specific Hebbian learning rules allows a network to continuously self-organize its weights during the lifetime of the agent (Najarro & Risi, 2020). We found that starting from completely random weights, evolved Hebbian rules enable an agent to navigate a dynamic 2D-pixel environment; likewise, the approach also allows a simulated 3D quadruped to learn how to walk while adapting to some morphological damage not seen during training and in the absence of any explicit reward or error signal in less than 100 timesteps.
Parameter Sharing in Self-Organizing Systems to Increase Generalization
The amount of information it takes to specify the wiring of a sophisticated brain directly is far greater than the information stored in the genome. Instead of storing a specific configuration of synapses, the genome encodes a much smaller number of rules that govern how to wire up a brain through a self-organizing process and how synapses should change based on the activation of neurons. This amazing compression has also been called the “genomic bottleneck” (Zador 2019), and neuroscience suggests that this limited capacity has a regularizing effect that results in wiring and plasticity rules that generalize well.
Iteratively merging learning rules. Inspired by the biological phenomenon of the genomic bottleneck and building on our previous meta-learning work (Najarro & Risi, 2020), we recently showed that by allowing multiple connections in a neural network to share the same local Hebbian learning rule, it is possible to drastically reduce the number of trainable parameters, while simultaneously obtaining a more robust agent (Pedersen & Risi, 2021). During evolution, by iteratively using simple K-Means clustering to combine rules, an approach we call Evolve & Merge was able to reduce the number of trainable parameters from 61,440 to 1,920, without increasing the number of training iterations.
Learning learning rules through self-organization. Instead of starting with a large number of rules and then merging them over time, it is also possible to directly start with a network with shared parameters. In work by Kirsch & Schmidhuber (2020), multiple smaller recurrent neural networks (RNNs) self-organize, resulting in the emergence of a global learning algorithm. The RNNs all have the same weight parameters but the internal hidden states can be different, allowing the network to learn its own learning algorithms. The self-organizing properties and sharing the same weights allow these networks to learn learning algorithms that generalize well. While this approach shows the great promise of self-organizing deep networks, it currently only works for small-scale problems and can get stuck in local optima. This fact points towards an open challenge with these types of self-organizing systems: they can be very hard to optimize. We will return to this challenge in the next section.
Learning to be robust to unseen and permutated sensory inputs. Incorporating ideas from self-organization has recently also allowed neural networks to become more resilient to disruptions in their inputs. In the work by Tang & Ha (2021), the inputs are fed into separate but identical neural networks, which can learn to integrate the locally received information (through a mechanism called attention) and still work even when the order of inputs is permutated. This paper points to another interesting research direction for self-organizing systems, which is how to best combine local and global information. Researchers have also recently shown that it is possible to directly use an NCA as a controller for an agent (Variengien et al. 2021); the NCA input cells receive information from the environment and the values of specific output cells are used to control the agent. Such as system also showed some robustness to noisy environments and unseen sensory inputs.
Controlling the Uncontrollable or How to train your Self-Organizing Systems
Throughout this post, we have seen that artificial self-organizing systems are able to display some of the benefits of their biological counterparts. At the same time, it is also becoming clear that these types of collective systems can be difficult to train, which is due to two main reasons: (1) The first is that these systems are hard to control. Because there is no one entity in charge, controlling a self-organizing system is to try to nudge it into the right direction or as Kelly (1992) puts it:
“Guiding a swarm system can only be done as a shepherd would drive a herd: by applying force at crucial leverage points, and by subverting the natural tendencies of the system to new ends.“
(2) These systems are unpredictable, which means there is no analytical mathematical model that could tell us directly the outcome of the self-organizing process. We know that we can not even predict the outcome of simple developmental systems directly, such as some 1D cellular automata (Wolfram 2002), but unfolding over time (i.e. actually running the program that grows the pattern) is necessary to observe the outcome. What is the case for simple 1D CAs also holds true for biological nervous systems, which need time and energy to unfold in an algorithmic process (Hiesinger 2021).
“The self-assembling brain knows no shortcuts.”
Hiesinger 2021
Searching for the parameters of self-organizing systems that produce particular patterns is thus a difficult optimization problem and trying to make self-organization programmable is a research field of its own, called morphogenetic engineering (Doursat et al. 2012, 2013). Researchers early on have used different types of genetic algorithms (Mitchell et al. 1996) and genetic programming (Miller 2004) to find the rules of CAs. While inspired by the open-ended evolutionary programming of biological systems, evolutionary algorithms can get stuck in local optima when tasked to find the rules to grow a particular target (Nichele et al. 2017). The benefit of gradient descent-based approaches is that we can efficiently train these systems to grow a particular target structure (Mordvintsev et al., 2020; Sudhakaran et al. 2021) but the target structure itself is thus fixed and not discovered by the NCA itself. In other words, the NCA is only trained to grow a given structure and not to discover new structures. Additionally, using gradient descent-based approaches requires backpropagating the gradients through the whole sequence of developmental steps. Thus this process becomes increasingly infeasible in terms of memory requirements with an increase in developmental steps.
An interesting recent alternative for searching for self-organized patterns in complex dynamical systems are more open-ended search methods such as quality diversity (QD) (Pugh et al. 2016) and intrinsically-motivated learning approaches (Baranes & Oudeyer 2013). In these methods, the idea is to not search for one particular solution (as is typical in machine learning) but instead try to find a maximally diverse set of outcomes.
For example, in the work by Earle et al. (2021) the authors use a variant of the QD algorithm MAP-Elites (Mouret & Clune, 2015; Fontaine et al. 2020) to evolve a whole population of diverse NCAs that can generate game levels for Sokoban and Zelda. Their approach searches over the space of levels that show different levels of symmetry and path-length and for these combinations tries to find levels that also satisfy some validity criteria (e.g. levels in Zelda must contain one player, one key, and one door). The benefit of MAP-Elites is that the discovery of NCAs able to generate levels with particular features can be stepping stones to generate high-quality levels in other parts of the search space. The property of QD algorithms to explore more of the search space than traditional objective-based approaches might be especially important for self-organizing systems with their complex fitness landscapes and many local optima. The authors also compare their NCA approach with another generative neural network method called Compositional Pattern Producing Networks (CPPNs; Stanley 2007) that describes the pattern indirectly but does not go through a process of iterative self-organization. They find that NCAs allow for a larger exploration of the level space, with individual NCAs having more diverse outputs. While a more exhaustive comparison on different domains will be important to draw definite conclusions, these results hint at some of the additional benefits of self-organizing representations compared to other generative methods.
Another example is the intrinsically-motivated deep learning approach by Reinke et al. 2020, which can find interesting patterns in the continuous Game of Life system Lenia (Chan 2020). The approach was originally developed for learning inverse models in robotics and is a combination of intrinsically-motivated goal exploration and an unsupervised learning approach based on a deep autoencoder that learns what constitutes interesting pattern features. The authors also use CPPNs but instead of encoding static patterns as in the previous example on level generation (Earle et al., 2021), here the CPPN only specifies the initial parameters of the system, which is then let to self-organize in subsequent rollouts.

Both the evolutionary-based quality diversity method and intrinsically-motivated learning approach are able to efficiently discover interesting patterns, suggesting that these types of approaches are promising for the hard-to-navigate search spaces of self-organizing systems. An important future research direction will be how to make the exploration of this search space more sample efficient.
Living systems can construct and repair themselves, learn robustly from varying sensory data, and still function in novel environments. The combination of deep learning with ideas from collective intelligence is recently starting to capture the interest of the larger machine learning community (including an exciting upcoming ICLR 2022 workshop). For a great overview also check out the very recent review paper by Ha and Tang (2021) on collective intelligence for deep learning. The merger of these ideas points the way towards more robust and resilient artificial systems. We can now grow complex 3D artifacts, simulated soft robots that can recover from damage, self-assembling modular robots that generalize to unseen morphologies, or neural networks that can deal with permutated inputs. By capitalizing on the same ideas that allowed biological systems to strive, we will be able to significantly expand the range of tasks we can apply our AI approaches to. However, self-organizing systems come with their own challenges, such as generally being less efficient, less controllable, unpredictable, and harder to train. An important future research direction is how to best mitigate these apparent disadvantages while exploiting their many benefits.
Please cite this work as:
@article{risi2021selfassemblingAI,
title = "The Future of Artificial Intelligence is Self-Organizing and Self-Assembling",
author = "Risi, Sebastian",
journal = "sebastianrisi.com",
year = "2021",
url = "https://sebastianrisi.com/self_assembling_ai"
}
References
Baranes, A., & Oudeyer, P. Y. (2013). Active learning of inverse models with intrinsically motivated goal exploration in robots. Robotics and Autonomous Systems, 61(1), 49-73.
Bozorgmehr, J. E. H. (2014). The role of self-organization in developmental evolution. Theory in Biosciences, 133(3-4), 145-163.
Camazine, S., Deneubourg, J. L., Franks, N. R., Sneyd, J., Theraula, G., & Bonabeau, E. (2020). Self-organization in biological systems. Princeton university press.
Chan, B. W. C. (2020). Lenia and expanded universe. arXiv preprint arXiv:2005.03742.
Davies, J. A. (2014). Life unfolding: How the human body creates itself. OUP Oxford.
Doursat, R., Sayama, H., & Michel, O. (Eds.). (2012). Morphogenetic engineering: toward programmable complex systems. Springer.
Doursat, R., Sayama, H., & Michel, O. (2013). A review of morphogenetic engineering. Natural Computing, 12(4), 517-535.
Earle, S., Snider, J., Fontaine, M. C., Nikolaidis, S., & Togelius, J. (2021). Illuminating Diverse Neural Cellular Automata for Level Generation. arXiv preprint arXiv:2109.05489.
Edelmann, J. B., & Denton, M. J. (2007). The uniqueness of biological self-organization: challenging the Darwinian paradigm. Biology & Philosophy, 22(4), 579-601.
Fontaine, M. C., Togelius, J., Nikolaidis, S., & Hoover, A. K. (2020, June). Covariance matrix adaptation for the rapid illumination of behavior space. In Proceedings of the 2020 genetic and evolutionary computation conference (pp. 94-102).
Gilpin, W. (2019). Cellular automata as convolutional neural networks. Physical Review E, 100(3), 032402.
Gleave, A., Dennis, M., Wild, C., Kant, N., Levine, S., & Russell, S. (2019). Adversarial policies: Attacking deep reinforcement learning. arXiv preprint arXiv:1905.10615.
Grattarola, D., Livi, L., & Alippi, C. (2021). Learning Graph Cellular Automata. Advances in Neural Information Processing Systems, 34.
Hamann, H. (2018). Swarm robotics: A formal approach. Springer.
Ha, D., & Tang, Y. (2021). Collective Intelligence for Deep Learning: A Survey of Recent Developments. arXiv preprint arXiv:2111.14377.
Hiesinger, P. R. (2021). The Self-Assembling Brain: How Neural Networks Grow Smarter. Princeton University Press.
Hiesinger, P. R. (2018). The Self-Assembling Brain: Contributions to Morphogenetic Engineering from a Self-Organizing Neural Network in the Insect Brain. In ALIFE 2018: The 2018 Conference on Artificial Life (pp. 202-203). MIT Press.
Hintze, A., Hiesinger, P. R., & Schossau, J. (2020). Developmental neuronal networks as models to study the evolution of biological intelligence.
Horibe, K., Walker, K., & Risi, S. (2021). Regenerating Soft Robots Through Neural Cellular Automata. In EuroGP (pp. 36-50).
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., … & Hassabis, D. (2021). Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873), 583-589.
Kelly, K. (2009). Out of control: The new biology of machines, social systems, and the economic world. Hachette UK.
Kirsch, L., & Schmidhuber, J. (2020). Meta Learning Backpropagation And Improving It. arXiv preprint arXiv:2012.14905.
Mitchell, M., Crutchfield, J. P., & Das, R. (1996). Evolving cellular automata with genetic algorithms: A review of recent work. In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA’96) (Vol. 8).
Miller, J. F. (2004). Evolving a self-repairing, self-regulating, french flag organism. In Genetic and Evolutionary Computation Conference (pp. 129-139). Springer, Berlin, Heidelberg.
Mordvintsev, A., Randazzo, E., Niklasson, E., & Levin, M. (2020). Growing neural cellular automata. Distill, 5(2), e23.
Mouret, J. B., & Clune, J. (2015). Illuminating search spaces by mapping elites. arXiv preprint arXiv:1504.04909.
Nguyen, A., Yosinski, J., & Clune, J. (2015). Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 427-436).
Nichele, S., Ose, M. B., Risi, S., & Tufte, G. (2017). CA-NEAT: evolved compositional pattern producing networks for cellular automata morphogenesis and replication. IEEE Transactions on Cognitive and Developmental Systems, 10(3), 687-700.
Pathak, D., Lu, C., Darrell, T., Isola, P., & Efros, A. A. (2019). Learning to control self-assembling morphologies: a study of generalization via modularity. arXiv preprint arXiv:1902.05546.
Pedersen, J. W., & Risi, S. (2021). Evolving and merging Hebbian learning rules: increasing generalization by decreasing the number of rules. arXiv preprint arXiv:2104.07959.
Pugh, J. K., Soros, L. B., & Stanley, K. O. (2016). Quality diversity: A new frontier for evolutionary computation. Frontiers in Robotics and AI, 3, 40.
Qu, X., Sun, Z., Ong, Y. S., Gupta, A., & Wei, P. (2020). Minimalistic attacks: How little it takes to fool deep reinforcement learning policies. IEEE Transactions on Cognitive and Developmental Systems.
Reinke, C., Etcheverry, M., & Oudeyer, P. Y. (2019). Intrinsically motivated discovery of diverse patterns in self-organizing systems. arXiv preprint arXiv:1908.06663.
Risi, S., & Togelius, J. (2020). Increasing generality in machine learning through procedural content generation. Nature Machine Intelligence, 2(8), 428-436.
Rubenstein, M., Cornejo, A., & Nagpal, R. (2014). Programmable self-assembly in a thousand-robot swarm. Science, 345(6198), 795-799.
Stanley, K. O. (2007). Compositional pattern producing networks: A novel abstraction of development. Genetic programming and evolvable machines, 8(2), 131-162.
Stooke, A., Mahajan, A., Barros, C., Deck, C., Bauer, J., … & Czarnecki, W. M. (2021). Open-ended learning leads to generally capable agents. arXiv preprint arXiv:2107.12808.
Su, J., Vargas, D. V., & Sakurai, K. (2019). One pixel attack for fooling deep neural networks. IEEE Transactions on Evolutionary Computation, 23(5), 828-841.
Sudhakaran, S., Grbic, D., Li, S., Katona, A., Najarro, E., Glanois, C., & Risi, S. (2021). Growing 3D Artefacts and Functional Machines with Neural Cellular Automata. arXiv preprint arXiv:2103.08737.
Tang, Y., & Ha, D. (2021). The sensory neuron as a transformer: Permutation-invariant neural networks for reinforcement learning. In Thirty-Fifth Conference on Neural Information Processing Systems.
Variengien, A., Nichele, S., Glover, T., & Pontes-Filho, S. (2021). Towards self-organized control: Using neural cellular automata to robustly control a cart-pole agent. arXiv preprint arXiv:2106.15240.
Vinyals, O., Babuschkin, I., Czarnecki, W. M., Mathieu, M., Dudzik, A., Chung, J., … & Silver, D. (2019). Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 575(7782), 350-354.
Wolfram, S. (2002). A new kind of science (Vol. 5, p. 130). Champaign, IL: Wolfram media.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., & Philip, S. Y. (2020). A comprehensive survey on graph neural networks. IEEE transactions on neural networks and learning systems, 32(1), 4-24.
Wulff, N., & Hertz, J. A. (1992). Learning cellular automaton dynamics with neural networks. Advances in Neural Information Processing Systems, 5, 631-638.
Zador, A. M. (2019). A critique of pure learning and what artificial neural networks can learn from animal brains. Nature communications, 10(1), 1-7.
Najarro, E., & Risi, S. (2020). Meta-learning through Hebbian plasticity in random networks. arXiv preprint arXiv:2007.02686.
Leave a Reply
You must be logged in to post a comment.